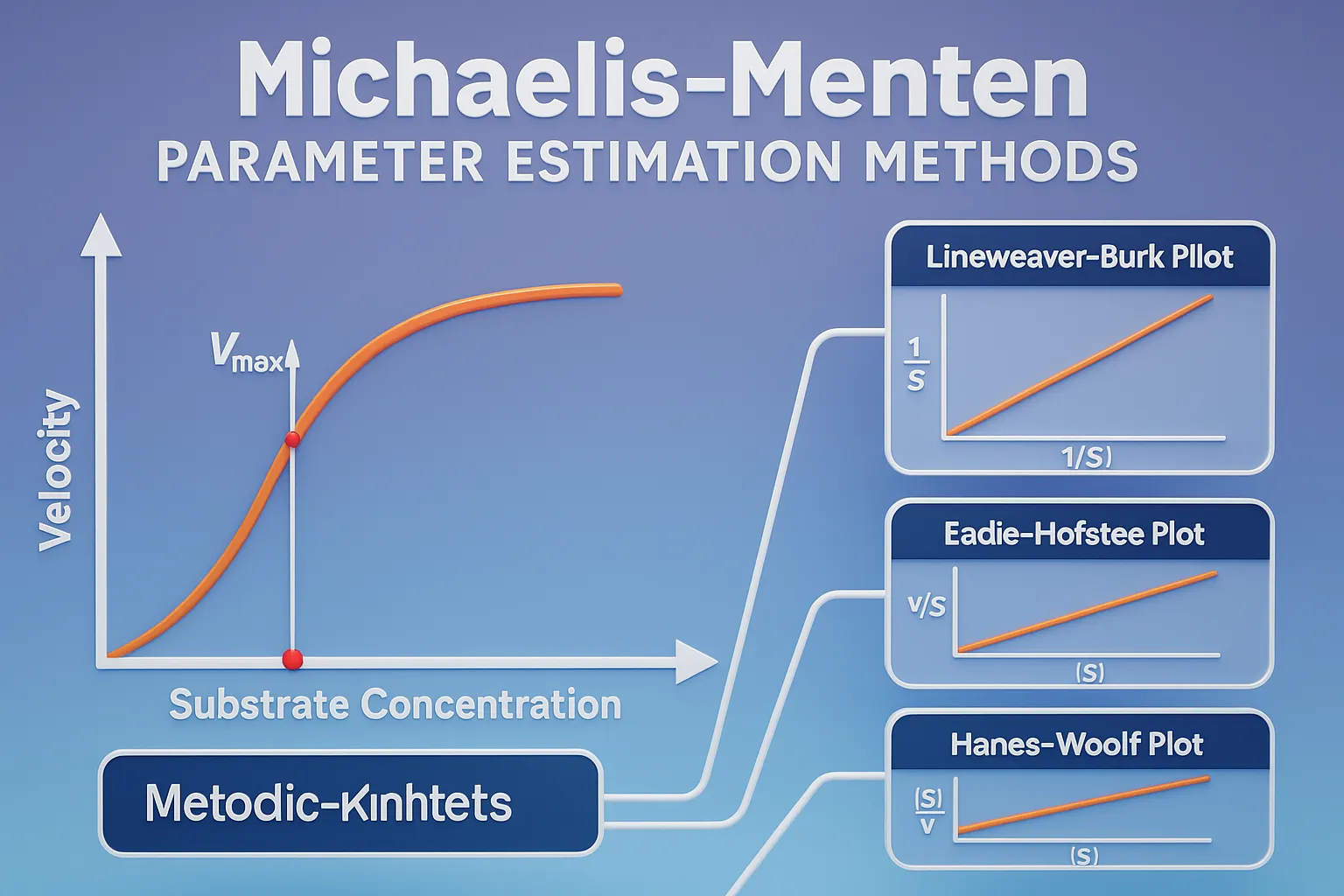
Michaelis-Menten Parameter Estimation Methods

Michaelis-Menten Parameter Estimation Methods determine Km and Vmax values using graphical and computational approaches.

Michaelis-Menten Parameter Estimation Methods

• Several methods estimate Vmax and Km from experimental data:

1. Lineweaver-Burk Plot (Double Reciprocal Plot)

   • By taking the reciprocal of the Michaelis-Menten equation:
     • $\frac{1}{V} = \frac{K_m}{V_{\text{max}}} \cdot \frac{1}{[S]} + \frac{1}{V_{\text{max}}}$
     • Plot 1/V 1/[S], resulting in a straight line.
     • Slope = Km/Vmax, y-intercept = 1/Vmax, x-intercept = -1/Km.
   • 

2. Direct Linear (Hanes-Woolf) Plot

   • Multiplying both sides of the Michaelis-Menten equation by [S] gives:
     • $\frac{[S]}{V} = \frac{[S]}{V_{\text{max}}} + \frac{K_m}{V_{\text{max}}}$
     • Plot [S]/V [S], yielding a straight line.
     • Slope = 1/Vmax, y-intercept = Km/Vmax.
   • 

3. Eadie-Hofstee Plot

   • Rearranging the equation:
     • $V = -\frac{V_{\text{max}}}{K_m} \cdot \frac{V}{[S]} + V_{\text{max}}$
     • Plot V V/[S], producing a straight line.
     • Slope = -Km, y-intercept = Vmax.
   • 

4. Hanes-Woolf Plot

   • Rewriting the equation:
     • $\frac{[S]}{V} = \frac{[S]}{V_{\text{max}}} + \frac{K_m}{V_{\text{max}}}$
     • Plot [S]/V [S].
     • Slope = 1/Vmax, y-intercept = Km/Vmax.
   • 

Click Here to Watch the Best Pharma Videos!