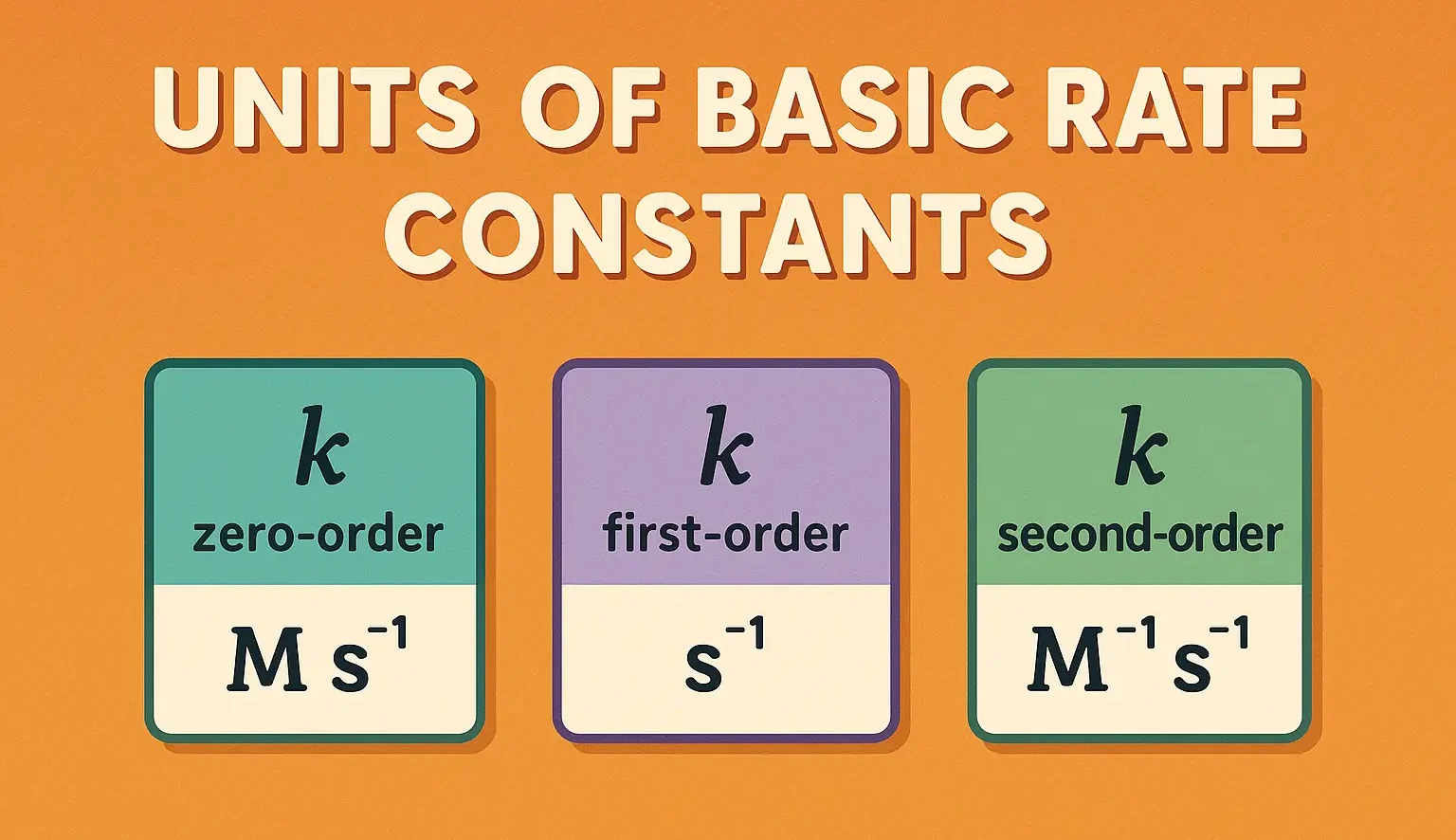
Effect of Temperature: As Temperature increases, the rate of degradation increases. Described by Arrhenius equation: $k = A \cdot e^{-\tfrac{E_a}{RT}}$ Where: k = rate constant A = frequency factor Ea = activation energy (J/mol or cal/mol) R = gas constant (8.314 J/mol·K or 1.987 cal/mol·K) T = temperature in Kelvin Implications: Helps estimate shelf life … Read more
Determination of Reaction Order defines how reactant concentration influences reaction rate. Determining the order of a degradation reaction involves monitoring concentration over time and fitting data to various integrated rate equations. Methods of Determination of Reaction Order: Graphical Method Plot concentration vs. time for different rate laws: Zero order: [A] vs. time (linear) First order: … Read more
The units of k depend on the reaction order. To ensure the rate has units of concentration/time (e.g., mol/L·s), units of k vary: Reaction Order Rate Expression Units of k Zero Rate = k mol·L⁻¹·s⁻¹ or concentration/time First Rate = s⁻¹ or time⁻¹ Second Rate = L·mol⁻¹·s⁻¹ or concentration⁻¹·time⁻¹v
First-Order Reactions are vital in drug stability, absorption, and pharmacokinetic studies. Definition: Rate of degradation is proportional to the concentration of the drug. Rate law: Derivation: Separate variables: $\text{Rate} = -\frac{d[A]}{dt} = k[A]$ Integrate both sides: $\frac{d[A]}{[A]} = -k \, dt$ Integrated form: $\int_{[A]_0}^{[A]} \frac{d[A]}{[A]} = -k \int_{0}^{t} dt$ $\ln [A] – \ln [A]_0 = … Read more
Pseudo-Zero Order Reactions are key in controlled drug delivery ensuring steady plasma levels. Not a true kinetic order, but appears zero-order due to constant concentration of one or more reactants. Occurs when a reactant is in large excess or is replenished (e.g., oxygen or water in excess). Often used in formulation studies where degradation appears … Read more
Zero-Order Reactions explain drug elimination like alcohol and phenytoin at saturating doses. Definition: Rate of degradation is independent of concentration. Rate law: \(\text{Rate} = -\frac{d[A]}{dt} = k\) Separate variables: \( d[A] = -k \, dt \) Integrate both sides: $\int_{[A]_0}^{[A]} d[A] = -k \int_{0}^{t} dt$ Graph: Plot of [A] vs. time = straight line with … Read more
Reaction kinetics sand Its Relevance to Drug Stability is the study of rates at which chemical reactions occur. In pharmaceuticals, it helps: Predict how long a drug remains stable Design appropriate storage conditions Optimize formulations Set expiration dates A general rate law expresses how the rate of reaction depends on the concentration of reactants. General … Read more
Definition of Drug Stability Drug stability refers to the ability of a pharmaceutical product to maintain its physical, chemical, microbiological, therapeutic, and toxicological specifications throughout its shelf life. A drug degrades over time due to: Chemical reactions (e.g., hydrolysis, oxidation, photodegradation) Environmental factors (light, temperature, humidity) Interaction with excipients or container Types of Stability: Chemical … Read more
Particle Number helps assess size distribution, stability, and quality in pharmaceutical formulations. Particle Number refers to the total count of discrete particles present in a given dispersion or sample. You can estimate the numbers of particles in a sample if the total mass, average particles diameter, and density are known. Formula $N = \frac{6M}{\pi D^{3} … Read more
Mean Particle Size affects dissolution, stability, flow, and bioavailability of pharmaceutical products. Mean Particle Size indicates the average dimension of particles in a sample for uniform analysis. Because particle populations contain a range of sizes, different types of mean particle sizes are used: 1. Arithmetic Mean Diameter(D₁) $D_1 = \frac{\sum_i n_i D_i}{\sum_i n_i}$ Where: $D_i … Read more
