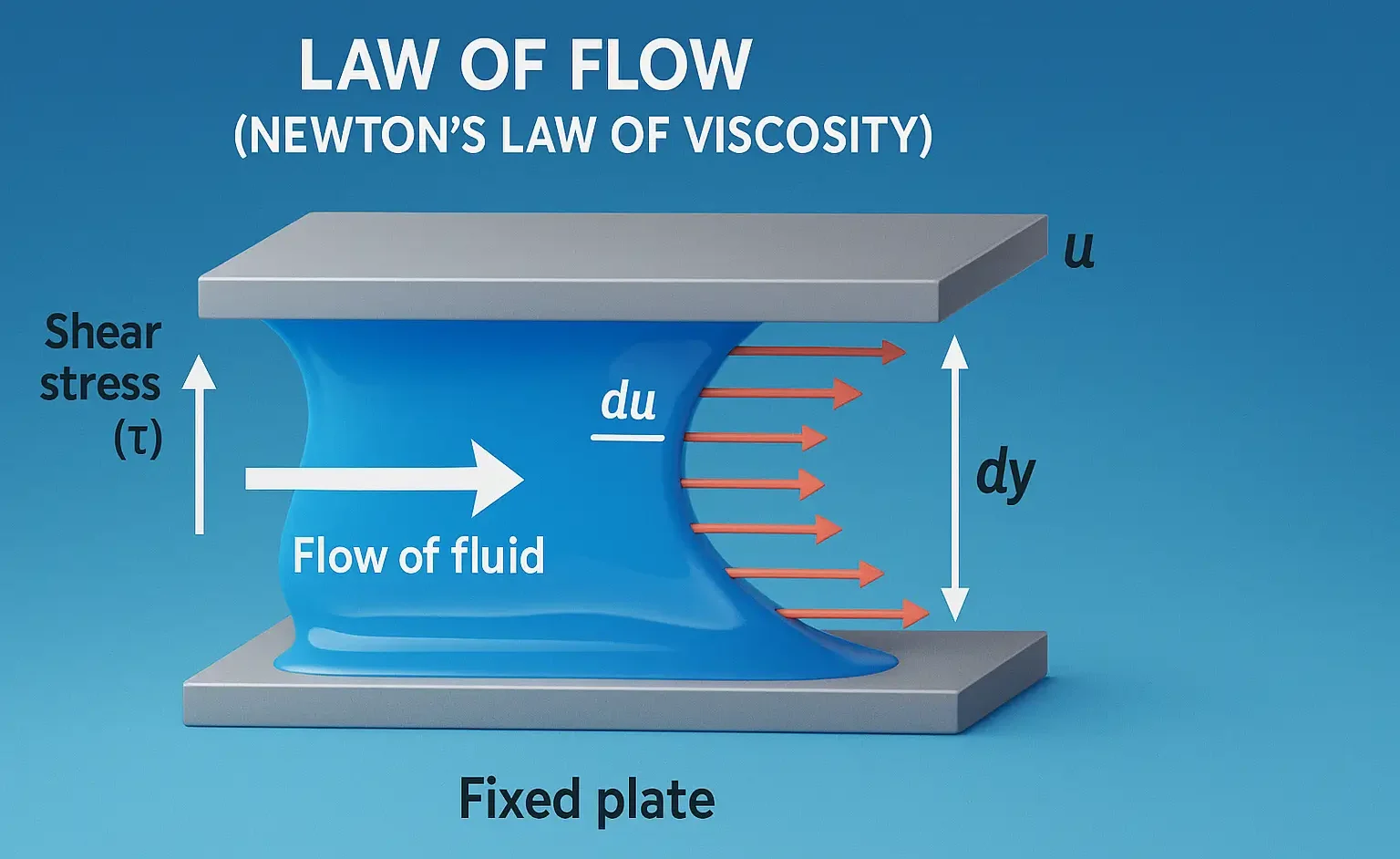
Law of Flow (Newton’s Law of Viscosity)

• Law of Flow (Newton’s Law of Viscosity) states shear stress is directly proportional to velocity gradient.
• Law of Flow (Newton’s Law of Viscosity) explains Newtonian fluid behavior in pharmaceutical systems.
• This refers to the application of Newton’s law in describing fluid behavior.

Newton’s Law (Restated):

$\frac{F}{A} = \eta \cdot \frac{du}{dy}$

Where:

• F/A = applied force per area = shear stress (τ)
• du/dy = velocity gradient = shear rate (γ)
• η (eta) = Viscosity (measure of internal resistance to flow)
• This law explains how a fluid flows under applied stress.

Assumptions for Newtonian Flow:

• Fluid layers move over each other with uniform velocity gradients.
• No yield stress (fluid begins to flow immediately upon stress application).
• Viscosity is constant at a given temperature and pressure.

Explanation:

• This equation states that the shear stress (F) needed to maintain flow in a fluid is directly proportional to the rate of shear. The constant of proportionality is the viscosity.

Units:

• Shear stress: dynes/cm² or Pascals (Pa)
• Shear rate: s⁻¹ (reciprocal seconds)
• Viscosity:
  • CGS system: poise (P), centipoise (cP)
  • SI system: Pascal-seconds (Pa·s)
  • 1 Pa·s = 10 P = 1000 cP

Thank you for reading from Firsthope's notes, don't forget to check YouTube videos!