Second-Order Reactions

• Definition: Rate depends on either:
• • Square of one reactant: $\text{Rate} = k[A]^2$
  • Product of two reactants: $\text{Rate} = k[A][B]$
• Integrated form (when A = B):

$\tfrac{1}{[A]_t} = \tfrac{1}{[A]_0} + kt$

Derivation:

Separate variables:

$\frac{d[A]}{[A]^2} = -k \, dt$

Integrate both sides:

$\int_{[A]_0}^{[A]} \frac{d[A]}{[A]^2} = -k \int_{0}^{t} dt$

$\left[ -\frac{1}{[A]} \right]_{[A]_0}^{[A]} = -kt$

$- \frac{1}{[A]} + \frac{1}{[A]_0} = -kt$

$\frac{1}{[A]} = \frac{1}{[A]_0} + kt$

• Graph: $\text{Plot of }\frac{1}{[A]}$ vs. time = straight line with slope = k

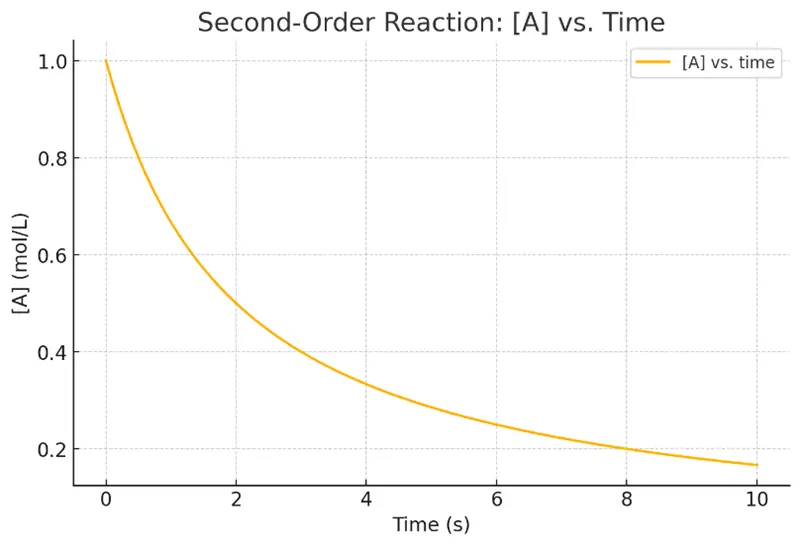
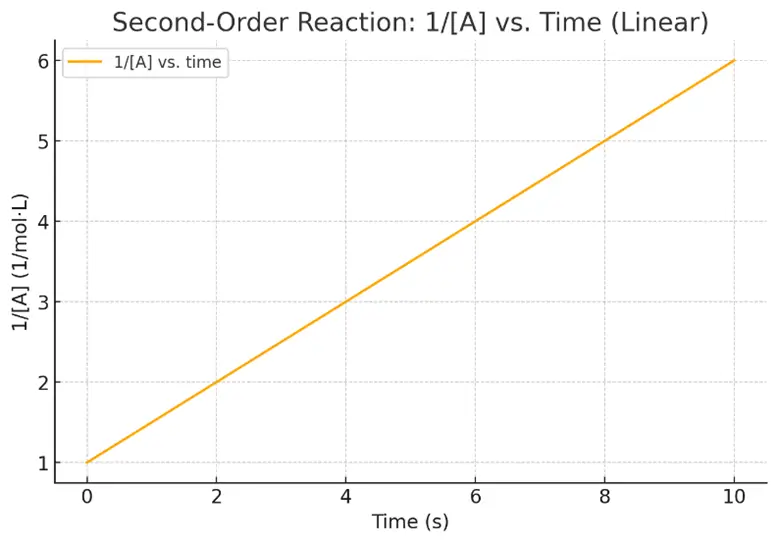
Features:

• Half-life depends on initial concentration:

$t_{1/2} = \frac{1}{k[A]_0}$

• Common in bimolecular reactions

Click Here to Watch the Best Pharma Videos!